Introduction

I am currently working through Stanford’s algorithms course as part of “learning my fundamentals”, and one difficult and interesting topic that I’ve encountered is computing strongly connected components of a directed acyclic graph.

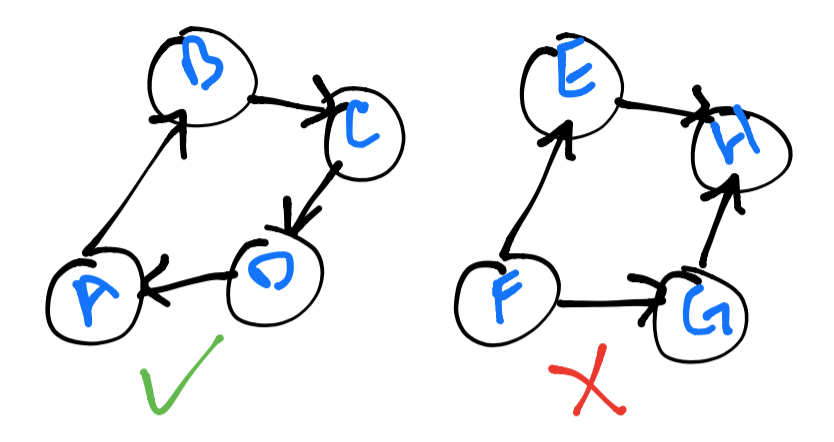
A graph is said to be strongly connected if every vertex is reachable from every other vertex. In the image below, you will notice that the left graph is strongly connected, but the right one is not – vertex H acts as a sink for every vertex with a connection and it is not possible to reach any other vertex from here.

Connected and not-so-strongly-connected graphs

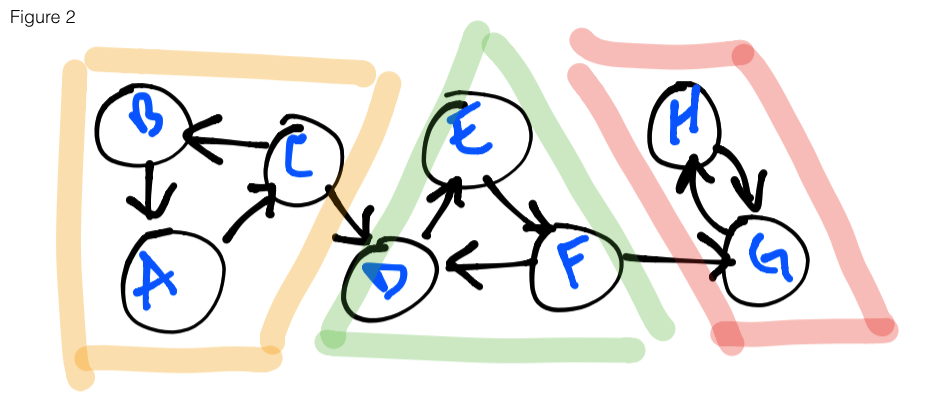
A graph can also contain multiple strongly connected components, each being a strongly connected subgraph.

In the figure 2 below, three strongly connected components (henceforth will be known by the abbreviation: SCCs) are highlighted: yellow, green and red. If a graph is entered at any vertex using depth-first search (DFS) as our traversal algorithm, it is possible to reach any of the vertices that are highlighted with the same color. For example, entering the graph at the vertex E, I am able to reach F and D. Likewise for vertex B with A and C, etc. You’ll also notice that there are some vertices that, upon exploration, can also lead to other components – this will be the crux of our problem today.

Example of strongly connected components

The problem

In figure 2 above, you’ll notice that if we start at vertex B, we are able to correctly explore all of the orange SCC. The problem arises when we start at A or C. There is a possibility that when we reach C the next vertex explored will be D and not B. If this occurs, we will incorrectly miss identifying the orange SCC. How then can we solve this problem? The astute observer will notice that for the red SCC, exploring any point will correctly identify the SCC. This is because there are no outbound edges – any point we hit will only explore the two vertices and that’s it. This is the fundamental understanding required to arrive at the solution.

Kosaraju’s two-pass algorithm

Kosaraju’s algorithm is a linear time algorithm to find strongly connected components. Our fundamental understanding will help us navigate this algorithm towards a solution. The algorithm solves this problem by going through the graph twice (using DFS): first through the transposed version of the graph (reversed), second through normally.

Why reversed? The first pass will collect the finishing times for all the vertices and compute a magical ordering. The second pass will go through the vertices in descending order of finishing times and compute the leaders.

The solution

To recap, the algorithm is composed of two parts:

  1. Loop through all vertices in the transposed graph – running DFS on each if it has not been explored and collecting the finishing time of each vertex
  2. Loop through all the vertices in the normal graph in descending order of finishing times – running DFS on each if it has not been explored and collecting the leader nodes

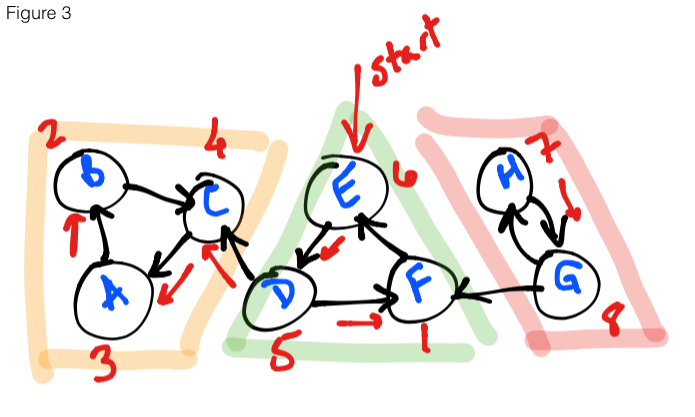
Step 1 SCC

Figure 3 shows the first step of the algorithm. Starting at E, we loop through the vertices on the reverse graph, running DFS on each vertex (if it has not been explored) and collecting the finishing times (denoted in red).

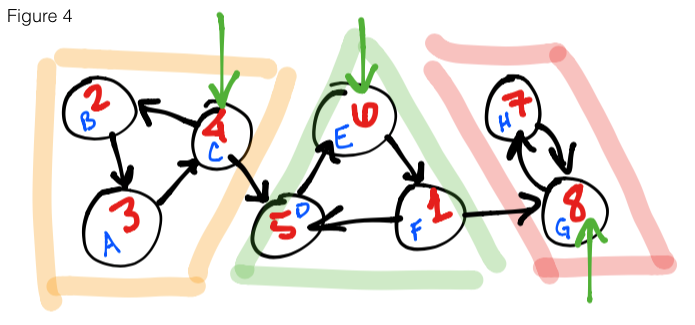
Step 2 SCC

Figure 4 shows the second step of the algorithm. We substitue the vertex names for their finishing times, un-reverse the edges, then start a DFS on the highest finishing time moving in descending order. In the figure, we start at 8 – marking it as leader node – then continue on to 7 and end this run because all reachable vertices have been explored. We move on to the next highest finishing time, 6, marking it as leader and explore all adjacent vertices. Once we are finished with this SCC, we see that the next unexplored vertex is 4, so we start there, mark it as leader and explore the final 2 vertices. As you might notice, the leaders we have collected are { 8, 6, 4 } (green arrows), and that is exactly the amount of SCCs in this graph.

Final thoughts

This was an interesting and difficult algorithm and has definitely given me confidence in working with graph-based problems. I wrote it in JavaScript using Node as my run-time environment for execution. It worked well enough for small datasets (using an adjacency list as my graph representation) but when I encountered larger datasets I ran into a lot of issues with stack and heap overflows as my implementation of DFS was recursive (I was also creating the reverse graph and storing it in memory). Even after optimizations (using a stack to store finishing times, using a hash table of sets for my adjancency list), I ended up needing to increase the maximum stack size as well as the heap size. These options can be found under V8 options. Ultimately, my run command became:

$ node --max-old-space-size=4096 --stack-size=10000 sccs.js
  • Heap size: --max-old-space-size
  • Stack size: --stack-size

I was able to get a solution in under 5 seconds with a dataset of 70mb. Once again, I owe all this to Stanford’s algorithm course and particularly the professor, Tim Roughgarden. He is an excellent teacher and I highly recommend the course.